Один из универсальных способов вычисления такого интеграла состоит в следующем. Рассмотренный нами подход к вычислению интегралов вида (5.32) впервые был предложен в работах Филона. Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении.

Определённым интегралом от непрерывной функции f(x) на конечном отрезке (где ) называется приращение какой-нибудь её первообразной на этом отрезке. Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.

Соотношение (5.2) может быть использовано для приближенного вычисления производной от функции, заданной как аналитическим выражением, так и таблично. Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно с помощью неопределенного интеграла по формуле Ньютона-Лейбница. Другой источник погрешности – неточности в вычислении подынтегральной функции в узловых точках и ошибки округления.

Из трех рассмотренных методов прямоугольников метод средних прямоугольников является наиболее точным. A – некоторое большое число. Вычисление первого интеграла на конечном отрезке не вызывает вопросов. Выбор числа A производят таким образом, чтобы в пределах допустимой погрешности вторым интегралом можно было пренебречь. На отрезках и подынтегральная функция не содержит особенностей и указанные интегралы могут быть вычислены любым из рассмотренных выше методов.

Если областью интегрирования G является прямоугольник: , , то для вычисления двойного интеграла можно использовать любую из рассмотренных выше формул. С повышением кратности интегралов резко возрастает объем вычислений и рассмотренный подход становится неэффективным. Теоретическое обоснование рассмотренного варианта метода Монте-Карло для вычисления интегралов состоит в следующем. Этот алгоритм также обобщается на кратные интегралы.

Замечание. При вычислении несобственных интегралов не стоит забывать о том, что иногда подходящая замена переменной интегрирования позволяет вообще избавится от особенности

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок – отрезком интегрирования. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции.

ПостояннаяСиз последующих вычислений исключается. Обычно для вычисления производных используют готовые формулы (таблицу производных) и к выражению (5.1) не прибегают. Однако в численных расчетах на компьютере использование этих формул не всегда удобно и возможно. В частности, функция может быть задана в виде таблицы значений (полученных, например, в результате численного расчета). Это соотношение называется аппроксимацией (приближением) производной с помощью конечных разностей (значения и в формуле (5.2) конечны в отличие от их бесконечно малых значений в (5.1)).

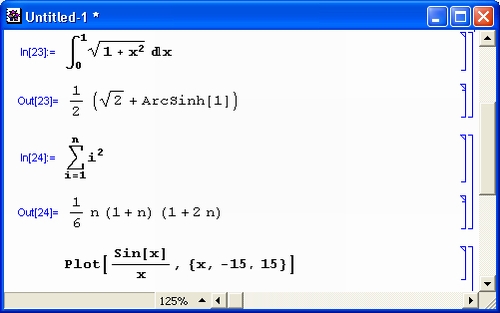
Таким образом, приближенное значение интеграла определяется суммой площадей прямоугольников, одна из сторон которых есть длина отрезка интегрирования , а другая – аппроксимирующая константа

В первом случае выбор величины произволен и определяется характером поведения функции. Для получения хорошей точности величину выбирают достаточно малой, такой чтобы на интервале функция была бы монотонна и менялась не существенно.

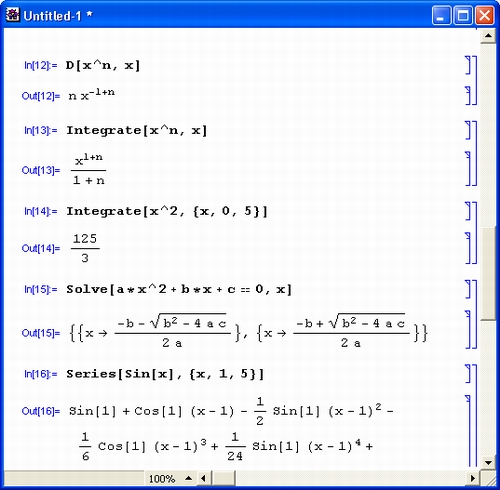
При этом, если количество узлов невелико и узлы расположены на большом расстоянии друг от друга, формула (5.2) может давать существенную погрешность. Сейчас обратимся к рассмотрению более общего подхода к задаче численного дифференцирования функции, заданной таблицей значений, в основе которого лежит использование интерполяционных полиномов. Однако на практике редко прибегают к аппроксимации функции одним интерполяционным полиномом, т.е. к глобальной интерполяции, в частности,из-за свойственной ей большой погрешности.

Мы получили простейшие приближенные формулы для первой производной от функции, заданной таблично. Эта форма записи интерполяционного полинома несколько отличается о ньютоновской, которая была рассмотрена ранее в главе 3 при описании кусочно-квадратичной интерполяции (формула (3.12)).

Используемые на практике методы численного интегрирования можно сгруппировать в зависимости от способа аппроксимации подынтегральной функции

Погрешность численного дифференцирования. 5.5) является формулой первого порядка точности. Рассмотренный пример, позволяет также сделать вывод о том, что погрешность формул численного дифференцирования зависит от того, в какой точке вычисляется производная. Другой источник погрешности численного дифференцирования связан с погрешностями вычисления значений функциив узлах и с погрешностями округлений при проведении расчетов на компьютере.

В этих случаях используют приближенные, методы интегрирования. Методы Ньютона-Котеса основаны на полиномиальной аппроксимации (интерполяции) подынтегральной функции. Алгоритмы этих методов просты и легко поддаются программной реализации. Сплайновые методы базируются на аппроксимации подынтегральной функции сплайнами. Такие методы имеет смысл использовать в задачах, где алгоритмы сплайновой аппроксимации применяются для обработки данных.

Погрешность, возникающая при численном интегрировании, также как и при численном дифференцировании, имеет два основных источника. Первым источником погрешности является приближенная замена подынтегральной функции аппроксимирующей функцией – погрешность аппроксимации.

Для вычисления каждого из интегралов в правой части можно использовать любой из рассмотренных выше методов. Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл.